【5分で読める】エンジニアのためのファイナンス入門　第３回　割引率の活用

2022/07/23 2022/11/03

mocha

【5分で読める】エンジニアのためのファイナンス入門は、全９回で構成されています。

エンジニアなどの技術系の専門職から、プロジェクトマネージャーやＣＴＯ・ＣＩＯ・ＣＤＯなどのビジネスサイドにステップアップするとき、多くの畑違いの新たな学びが必要となります。

特に、財務会計のスキルは、共通言語として必須になります。

経営資源の主要な要素の一つである「資金」を「調達」し「運用」する「ファイナンス」について、図表を用いてわかりやすく概説します。

社内研修やＯＪＴ等で、十分な学習機会を得ることができなかった境遇にある場合には、是非お役立てください。

この記事の特徴

●「５分で読める」ような工夫に努めております

●「図表」を使い、わかりやすい説明をこころがけています

●文献や論文の「参照箇所」を明示し、品質の担保に努めています

●お時間のあるときに、「参照箇所」を読んで理解を深めることができます

【5分で読める】エンジニアのためのファイナンス入門｜バックナンバー

第１回　企業活動とファイナンス

第２回　現在価値と将来価値

第３回　割引率の活用　：現価係数　✅今回

第４回　ＣＡＰＭ　：株主資本コスト

第５回　ＷＡＣＣ　：加重平均資本コスト

第６回　ＦＣＦ　　：フリーキャッシュフロー

第７回　ＮＰＶとＩＲＲ　：正味現在価値と内部収益率

第８回　継続価値　：ゼロ成長モデルと永続成長モデル

第９回　企業価値の算定

世の中には多くの考え方があります。

わたしたちの考えが、独善的な思い上がりに陥らないよう、一定の社会的な同意を与えてくれ、帰納的に援護してくれた言葉や内容を明示します。

「出所」とともに「参照箇所一覧」に整理いたしました。

割引率の活用

第３回は、「割引率の活用」です。

最初に、「現在地：全体と部分」を、図表でわかりやすくご案内します。

下の図をご覧ください。

今回は、割引率の活用についてご案内します。

↓　クリックして拡大

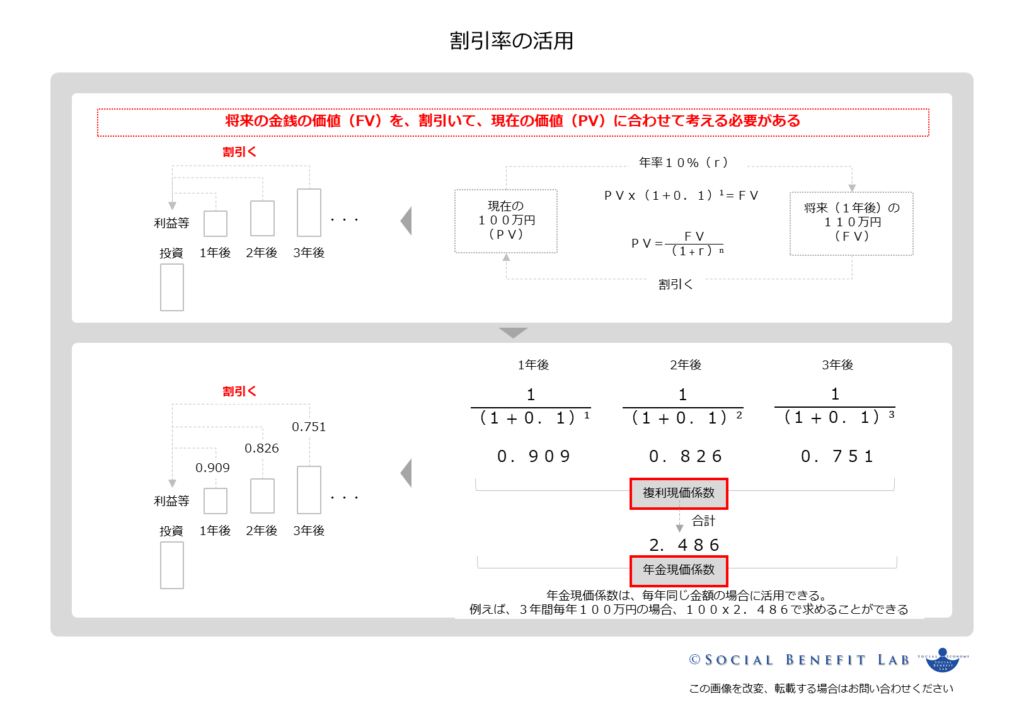
それでは、「割引率の活用」の本題にはいります。

結論は、以下のように示すことができます。

●「割引率」を繰り返し使う場合は、「現価係数」を求めておくと便利です

●よく使う「現価係数」は、「複利現価係数」「年金現価係数」です

●「現価係数」は、「１÷（１+ｒ）^ｎ」で求めることができます

●「複利現価係数」は、利息の再運用を考慮した複利計算に使う係数です

●「年金原価係数」は、毎期一定の金額を見込む場合に活用する係数です

●「複利現価係数」を求めて、それらを合計することで、「年金現価係数」を導出することができます

上記の「割引率の活用」の定義について、「参照」した箇所は、以下の参照箇所一覧をご覧ください。

ファイナンスに携わるようになると、「将来価値」を「現在価値」に合わせるための「割引率」を頻繁に利用することになります。

例えば、一定期間の「資金」の推移の「現在価値」を、複数の「割引率」で検討してみるなどの場面に遭遇することになると思います。

そのような場合には、あらかじめ「現価係数」を求めておくと便利です。

「現価係数」は、「１÷（１+ｒ）^ｎ」で求めることができます。

具体例として、割引率１０％の場合の「現価係数」は、

１年目は、１÷（１．１）^１≒０．９１
２年目は、１÷（１．１）^２＝１÷（１．１ｘ１．１）≒０．８３
３年目は、１÷（１．１）^３＝１÷（１．１ｘ１．１ｘ１．１）≒０．７５

上記の数字を、「複利現価係数」と呼びます。

こうして、「複利現価係数」を求めておけば、「資金」の額が異なる複数案の検討も、スムーズにできます。

例えば、１年目１００万円、２年目１５０万円、３年目２５０万円の収益が見込める案で、割引率が１０％の場合の「現在価値」を検討する場合、

１年目　１００万円　ｘ　０．９１　＝　９１万円
２年目　１５０万円　ｘ　０．８３　≒　１２５万円
３年目　２５０万円　ｘ　０．７５　≒　１８８万円
現在価値の合計は、（９１＋１２５＋１８８）＝４０４万円　也

上記で求めた「複利現価係数」を合計した値が、「年金現価係数」になります。

「年金現価係数」は、毎期一定の金額を見込む場合に活用できます。

例えば、１年目１００万円、２年目１００万円、３年目１００万円の収益が見込める案で、割引率が１０％の場合の「現在価値」を検討する場合、

「年金現価係数」は、０．９１+０．８３+０．７５＝「２．４９」
現在価値の合計は、毎期１００万円　ｘ　２．４９　＝　２４９万円　也

「複利現価係数」で計算しても、「年金現価係数」で計算しても、結論は同じになります。

抽象化して考えると、

ＡｘＢ + ＡｘＣ + ＡｘＤ　＝　Ａ（Ｂ+Ｃ+Ｄ）　になります
Ａは、毎期同じ金額
（Ｂ+Ｃ+Ｄ）は、「複利現価係数」を合計した「年金現価係数」

次回は、「割引率」を求めるために必要になる、「株主資本コスト」の求め方をご案内します。

今回は、これで終わりになります。

お読みくださりありがとうございました。

参照箇所一覧は、お時間のあるときにご参照ください。

【PR】わたしたちの体験談　おすすめ

Web製作の経験がなくても、簡単な設定で、
あっという間にこのサイトを立ち上げることができました。

毎日、WordPressで、記事を投稿しています。

このサイトは、【ConoHa WING】で、安定的に運用できています。

【PR】わたしたちの体験談　おすすめ

無料で、開業手続きができました。電子申請でしたので、自宅からあっという間でした。

その後、freee会計と、事業用のfreee Masterカードで、経理業務の負荷が大幅に軽減されました。

カードの利用履歴は、freee会計に、自動登録されます。あとは、確認して承認するだけ。

確定申告も、あっという間に終わりました。

freeeは、本業に専念するための力強い味方です。

参照箇所　一覧

「ファイナンシャル・マネジメント」　ロバート・C・ヒギンズ　グロービス経営大学院

■参照した主な内容
・財務諸表
・資金調達
・DCF法
・ROE、ROA、ROIC、EVA
・CAPM、WACC、NPV、IRR、FCF、ゼロ成長モデル、永続成長モデル、タックスシールド
参照　：　「ファイナンシャル・マネジメント」　ロバート・C・ヒギンズ　グロービス経営大学院　

リンク

「バリュエーションの教科書」　森生明　グロービス経営大学院教授

■参照した主な内容
・財務諸表
・ROE、PER、PBR
・DCF法、EVA、FCF、NPV、IRR
・WACC、β値、CAPM
・継続価値、ゼロ成長モデル、永続成長モデル
・デュポン式
・EBITDA倍率
・コングロマリットディスカウント
・M&A、垂直統合、水平統合
・現代ポートフォリオ理論、ブラックショールズモデル
・オプション、コール、プット
・リアルオプション
参照　：　「バリュエーションの教科書」　森生明　グロービス経営大学院教授　